电压跟随器为什么容易产生振荡？
运算放大器（op-amp）放大电路通常采用负反馈。 然而，运算放大器有一个极点（过渡点），可能会导致带宽内的相位滞后，从而产生正反馈。然而，电压跟随器（单位增益放大器）采用全反馈，其带宽延伸至截止频率，从而容易产生振荡。 使用电压跟随器时，必须选择以单位增益运行的产品。
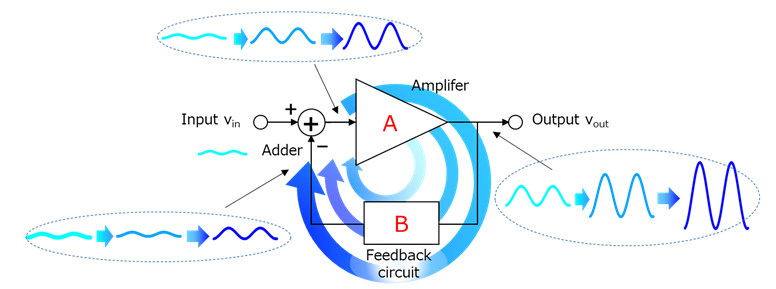
在使用运算放大器（op-amp）的放大电路中，通常采用反馈回路。然而，在某些条件下，这些反馈回路可能会导致振荡。这种现象称为振荡条件，具有增益和相位判据等特征。简单来说，如图所示，当输入信号或噪声通过反馈逐渐放大时，就会产生振荡（见图1）。
从数学角度来看，可以表达如下：
β×A ≧ 1
∠ β×A ≧ 360°
换言之，当反馈大于原始输入的信号并且同相相加时，就会产生振荡。
让我们用图表来说明独立运算放大器（op-amp）的频率特性。
增益曲线和极点：
- 运放的增益曲线显示了极点（过渡点）。
- 从第一个极点频率开始，增益按-20dB/十倍频程的斜率减小。
- 如果有两个极点，则第二个极点频率会产生-40dB/十倍频程的更大斜率。
- 此外，对于单极点，该极点频率下的相移延迟了90°。
- 对于两个极点，总相移达到180°。
单位增益和相移：
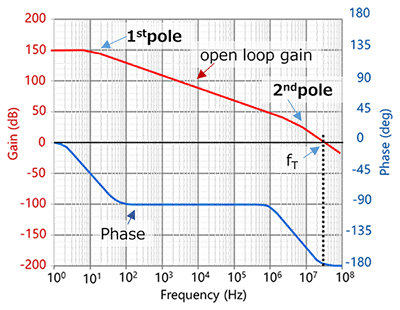
- 在并非专门为单位增益运算而设计的常用运放中，在截止频率（过零频率）（f_T）之前的带宽内有两个增益极点。
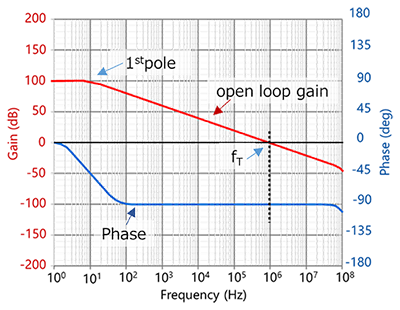
- 然而，专门为单位增益运算而设计的运放通常在带宽内只有一个极点。
- 因此，相移仅限于90°。
这些特性对于理解运放的行为至关重要，尤其是在设计反馈电路时。单位增益频率和相移在确定运放电路的可用频率范围方面具有至关重要的作用。
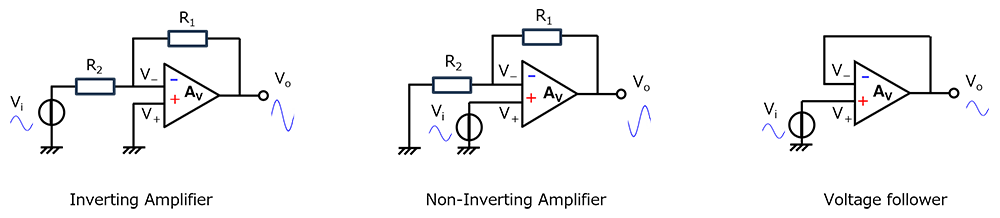
运算放大器（op-amp）通常用于两种主要类型的放大电路：反相放大器和同相放大器。电压跟随器亦称为单位增益放大器，属于同相放大器类别。在电压跟随器中，同相放大器的增益设为0dB（（R_1＝0）和（R_2＝∞））。
这两种放大器的工作原理如下：
同相放大器：
- 在同相放大器中，输入施加到正极端子，反馈来自负极端子。
- 由于输入连接到运放的正极，因此相从0°开始（类似于独立运放的频率响应）。
- 随着频率增加，相移从0°变为+180°。
反相放大器：
- 在反相放大器中，输入施加到负极端子，反馈来自输出。
反相放大器中的相移从+180°开始，并随着频率的增加而减小。
电压跟随器为全反馈同相放大电路，反馈速率为100%。其频带增益为0dB，截止频率为fT。由于输出反馈到负极端子形成负反馈，如果在频带内相延迟180°，则在该频率处会出现正反馈，从而产生振荡。
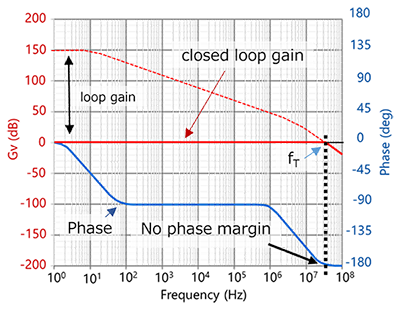
不保证单位增益的运算放大器以及保证单位增益的运算放大器的电压跟随器的相如下。截止频率处相位滞后最大，在下图（图5）所示的示例中，接近-180°，几乎没有相位裕度。（其可能为零，具体取决于产品。）
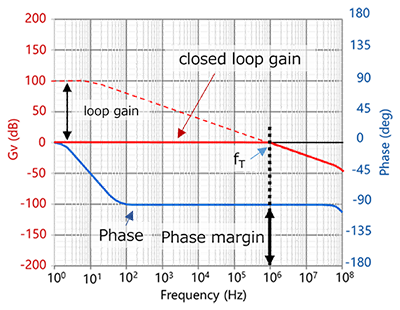
另一方面，具有保证单位增益的产品的相位裕度为90°。（图6）
然而，这是没有电容性负载时的情况。实际上，由于存在运算放大器的输出电容、接线的杂散电容以及负载侧的电容，因此可能会出现进一步的相位滞后。因此，可以说，没有单位增益保证的产品很有可能会发生振荡。
即使是保证单位增益的产品，如果负载电容很大，或者包含负载电容和输出阻抗的LPF的截止频率低于运算放大器的fT，或者在运算放大器的fT附近，也可能会发生振荡。
相关链接
FAQ
e-learning
应用说明
以下文档也包含相关信息。
Company names, product names, and service names used in this FAQ may be of their respective companies.