运算放大器使用的最大频率是多少？

如果所用频率的转换速率较低，则方波将变为梯形波，正弦波将变为三角波。
在高于开环增益3dB截止频率的频率处，电压增益会降低。 在这部分中，不仅电压增益因数因产品而异，而且如果输入宽带宽的信号，放大因数的梯度会导致波形失真。 请对运算放大器施加负反馈，以便增益在工作频带内保持平稳。
另外，请注意接近单位增益的频率下的振荡。请参考运算放大器e-learning 2.3振荡

 运算放大器e-learning 2.3振荡.  

• 转换速率（SR）：

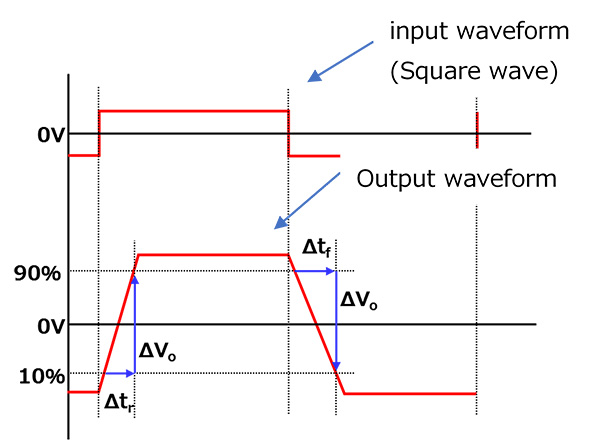
即使将理想的矩形波形（快速上升信号）施加到运算放大器的输入，其输出也不会提供理想的矩形波形，如图 3 所示。
每1μs输出电压的变化称为转换速率。
如图3所示，在运算放大器具有低转换速率的情况下，矩形输入信号在输出处表现为梯形信号，而正弦输入信号在输出处表现为三角形信号。

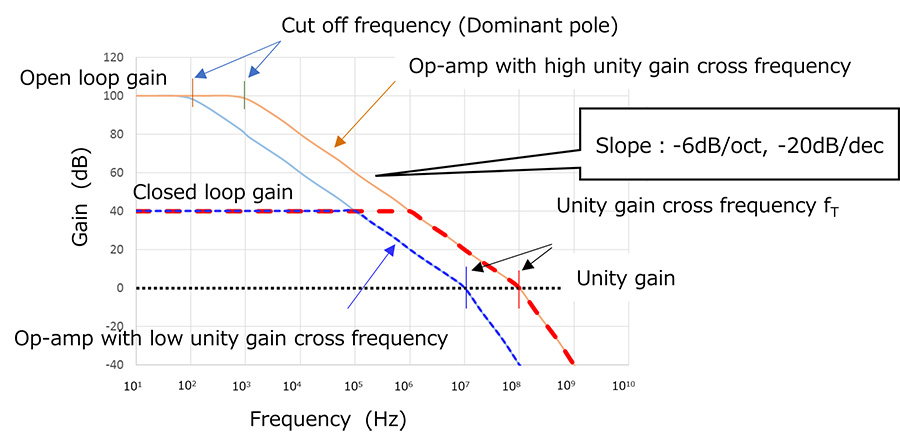
• 单位增益交叉频率（f_T）：

开环增益变为单位增益（0dB）的频率
如图2所示，截止频率较高的运算放大器可在闭环增益相同的情况下提供更大的带宽。

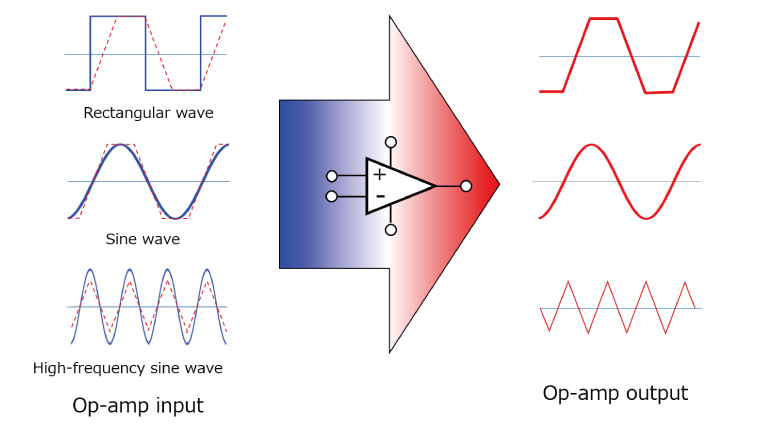
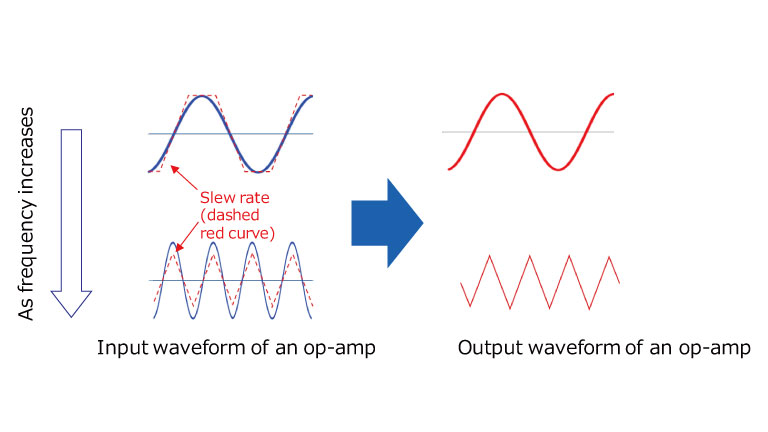
如果使用压摆率低的运算放大器，波形的形状会发生变化，并且失真会进一步恶化。
可利用压摆率计算出最大输出频率（f_max）。为简单起见，我们首先解释在单位增益下使用运算放大器的情况。
用下列公式表示压摆率（SR）：

SR＝ΔV_o/Δt_r或ΔV_o/Δt_f

当按时间区分的输出信号的最大值大于此SR时，就会发生波形失真。
设具有振幅A的输入正弦波的电压为Vin＝Asinωt。随后，如果输入信号振幅的最大变化（微分值）小于压摆率，则不会发生波形失真。
由于输入信号的微分值为dVin/dt＝Aωcosωt，故其最大值为Aω。因此，不会导致压摆率引起的波形失真的最大频率的理论计算公式如下，其中A为输入振幅。

SR＝Aω　＝2πf_maxA
f_max＝SR/2πA

若无单位增益，则用放大电路的电压增益乘以A_v，即V_o＝A_v x V_in
单位增益也按照此方法。

dVout/dt＝AvAω cosωt
SR＝AvAω　＝A_vA2πfmax
fmax＝SR/2πAA_v

实际上，有必要设置f_max，为所需频率预留足够的余量。